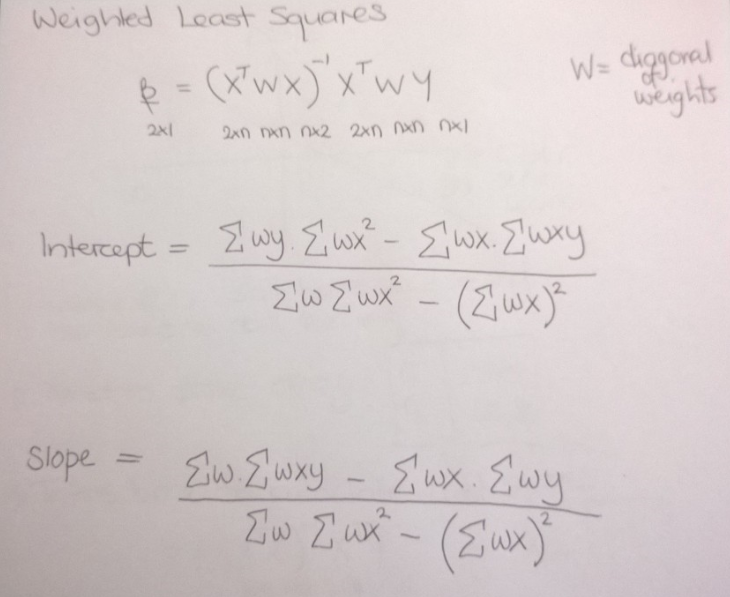Before I begin you probably should look at PID controllers. Proportional Integral Derivative controllers which appear common in control theory.
These PID controller require calibration and I have not reached doing that remotely. The logic below might be enough for my purpose, but if not then it
should help with the D part of the PID controller.
Rudder calculations
 to check rudder logic click here.
to check rudder logic click here.
A problem is that when the rudder is positioned in the center, the boat does not move in a straight line.
The different forces on the boat means that some helm (off center rudder position) is need.
The other issue is that for a given rudder position, the (small model) boat rate of change per second is fairly random.
Again forces are affecting the boat. However on average, stear left the boat does go left and vice versa.
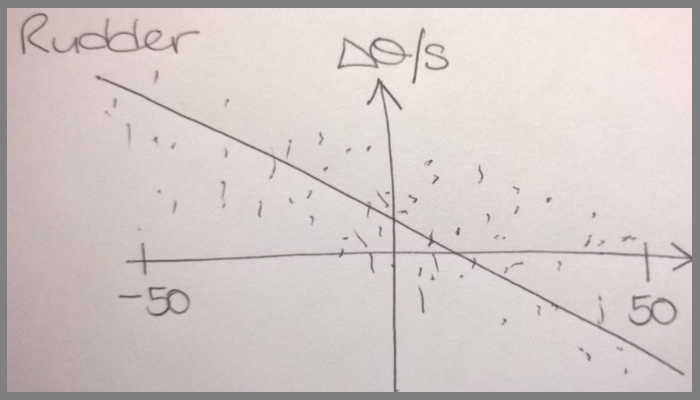
Some linear regression should help
Least Squares
Lets assume every one second, the boat records the rudder position and the last second change in heading. Very quickly the boat will
have a matrix nx2 of observations. A linear regression calculation can be performed to calculate the intercept and slope. Job done.
But can it be done better? Can we save memory (on a microcontroller) and save CPU time? Can we give more weight to the most recent observations?
Weighted Least Squares
In classical least squares each observation is given equal weights. Probably committing tonnes of statistical properties, but the
formula can be generalised to non equal weights. Here I am imagining the most recent observations are given higher significant in the
calculations. I have also expanded the matrix notation into the primative x,y and w. The motivation is to understand the calculations
better and to later reduce the number of calculations.
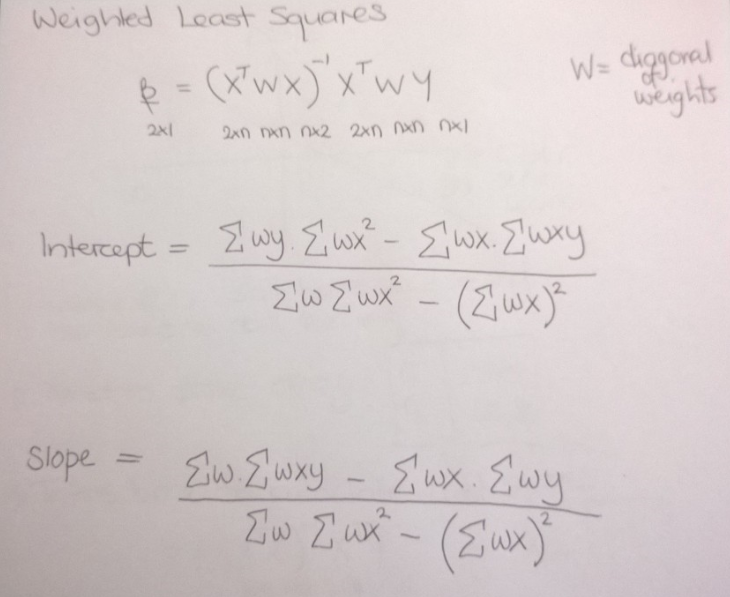
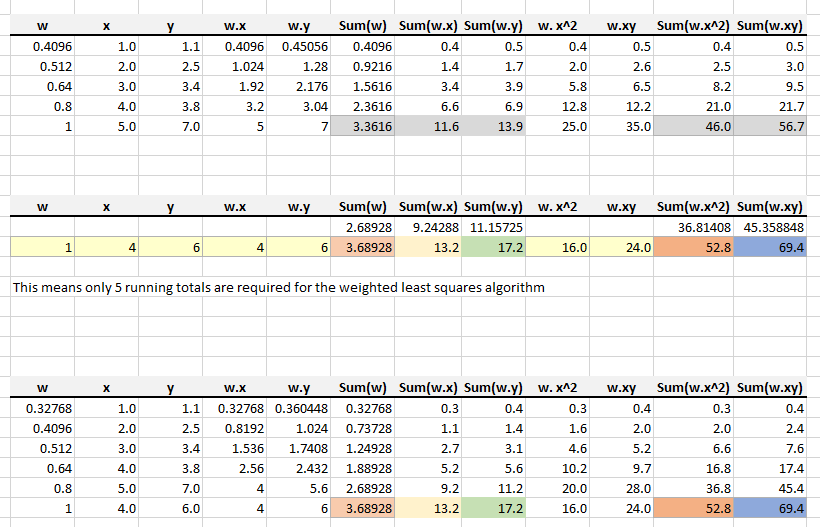
Exponential Weight Decay
Now a trick. Lets assume that the importance of each observation (rudder,change in heading) reduces exponentially in the least squares fit.
This means the summations from the last second calculation are multiplied by a number less than 1, say 0.90. Thus to calcuate the new regression line only
the new observation is required and not calculating from the first observation. Just work out the change and not the whole lot again. This saves memory and CPU time.
Rudder calculations
 to check rudder logic click here.
to check rudder logic click here.
Rudder.h
Rudder.cpp
WeightedLeastSquares.h
WeightedLeastSquares.cpp
 to check rudder logic click
to check rudder logic click